Bivariate Causal Inference
TLDR
I give a very short introduction to the idea of “causality” in statistics, then talk about two ways to infer causal structure for two variables - i.e, without using conditional independence statements. The ideas here are mostly taken from Peters, Janzing, and Schölkopf: Elements of causal inference: foundations and learning algorithms.
What is causality?
A “causal statistical model” is something like this:
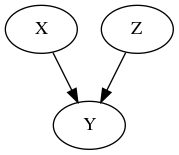
Or this
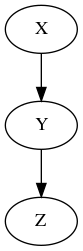
Where a classical statistical model tells you what the probability of various outcomes are, (which you can then use to derive conditional probabilities, etc), a causal model gives you more information - it tells you how the distribution changes when the system is intervened on. For instance, in the first model above, intervening on \(X\) has no effect on the distribution of \(Z\), whereas in the latter, the distribution of \(Z\) after the intervention \(X := x_0\) is exactly the conditional distribution \(P(Z=z|X=x_0)\).
Causal inference by conditional independence
We can actually distinguish between the two causal structures above without doing interventional experiments. This is because in the first model, \(X\) and \(Z\) are independent, but don’t (necessarily) remain independent after conditioning on \(Y\). For instance, if \(Y = X+Z\), learning that \(Y\) has a certain value tells us exactly how to compute \(X\) and \(Z\) from each other. On the other hand, in the second model, \(X\) and \(Z\) are not (necessarily) independent, but after conditioning on \(Y\), they are. That’s because the dependency of \(Z\) on \(X\) only “goes through” \(Y\), so if we already know what \(Y\) is, learning about \(X\) tells us nothing about \(Z\).
Why are \(X\) and \(Z\) independent in the first model? This is because of a basic principle of causal modeling, which we can paraphrase as “all (conditional or unconditional) dependencies between variables must be explained by causal structure”. (Formally, the distribution has the markov property with respect to the graph).
Bivariate causal inference
We can use conditional (in)dependence to try to tell causal graphs apart. But we can’t always do this. For instance, this graph:
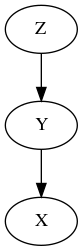
Gives rise to exactly the same independence statements as graph 2 above. (We say they are “Markov equivalent”). The worst case is the case where we have just two variables - since both graphs \(X \to Y\) and \(Y \to X\) are Markov equivalent. (And the third possible DAG, \(X\ Y\), corresponds to the statement that \(X\) and \(Y\) are independent - not very interesting).
How can we get around this problem, and detect causal structure when we only have two variables? Let’s make it concrete, and say that \(X\) is a variable that measures whether or not a person smokes, and \(Y\) measures cancer. We observe a strong correlation. We have supposed there are no confounding variables, but now we still have the question: does smoking cause cancer, or does cancer cause smoking?
Do an interventional experiment
The easiest way is to just test our theory directly against nature. The difference between the statements \(X \to Y\) and \(Y \to X\) is whether or not doing the intervention \(X := x_0\) will affect \(Y\) or not. In other words, we can take a large number of people, randomly assign them to either smoke or not smoke, then come back a few years later and see whether the smokers have more cancer. This experiment may not get past the ethics board.
Use domain knowledge
The idea that cancer causes smoking seems pretty dumb. People generally start smoking, then develop cancer many years later. We could try to build this idea into a more complicated causal model (with more variables), which we could statistically test, but we could also just take seriously the fact that the hypothesis “cancer causes smoking” is prima facie much less plausible than “smoking causes cancer”.
These two solutions are both pretty unsatisfying. Fortunately, we also have more sophisticated tools.
Independent mechanisms.
The basic idea is this: if the causal structure is that smoking causes cancer, then whatever process turns smoking into cancer is independent of the process that makes people smoke. This means that learning the conditional distribution \(P(\mathrm{Cancer}|\mathrm{Smoking})\) tells you nothing about the distribution \(P(\mathrm{Smoking})\) itself. On the other hand, learning the smoking rates of cancer victims and non-cancer victims does in fact tell you something about the cancer rate. This is called “The principle of independent mechanisms”. The “mechanisms” in question are the distributions \(P(\mathrm{Smoking})\) and \(P(\mathrm{Cancer}|\mathrm{Smoking})\). They are “independent” in the sense that each contains no information about the other. From this principle, we can derive some algorithms for testing the causal relationship.
Semi-Supervised Learning
Suppose we try to train a machine learning algorithm to predict whether a person has cancer based on whether or not they smoke. We provide the algorithm with a number of samples \((X_i,Y_i)\), each consisting of a “smoking?” and a “cancer?” measurement. We also provide it with a number of unlabeled samples, \(X_j\), with only the “smoking?” measurement. This is sometimes called “semi-supervised learning”. Do these extra samples help the algorithm? The principle of independent mechanisms says “no”. These samples only provide information about the distribution \(P(\mathrm{Smoking})\), which gives no information on the conditional \(P(\mathrm{Cancer|Smoking})\). On the other hand, if we’re trying to predic smoking from cancer, knowing something about the general cancer rate may actually help. Thus we can try to distinguish \(X \to Y\) and \(Y \to X\) from each other by seeing whether adding the unlabeled samples helps or not.
Independent noise
Linear models are ubiquitous in statistics. A linear model for \(X \to Y\), based on the principle of independent mechanisms, may look like this:
- \(X := a + bN_1\)
- \(Y := c + dX + eN_2\)
- \(N_1,N_2 \sim \mathcal{N}(0,1)\)
- \(N_1,N_2\) independent.
In other words, \(X\) is normally distributed, then \(Y\) is a sum of \(X\) times a constant and another normal distribution. The crucial property of this model is the independence of the noise variables. If we run a linear regression to predict \(Y\) from \(X\), we will get an error term of (on average) \(eN_2\) - this is independent of \(X\). But in the other direction, we get \(X = Y/d - c/d\) with an error term of, on average, \(\frac{e}{d} N_2\) - which is not independent of \(Y\) (since \(Y\) depends on \(N_2\)). Hence we can find the causal direction by running two linear regressions and seeing when we get an independent noise term.