Chu spaces and linear logic

A Chu space over \(S\) consists of a pair of sets \((X,U)\), and a function \(e: X \times U \to S\). A map of chu spaces \((X,U,e) \to (Y,V,e')\) is a pair of maps \(X \to Y, V \to U\) so that the diagram

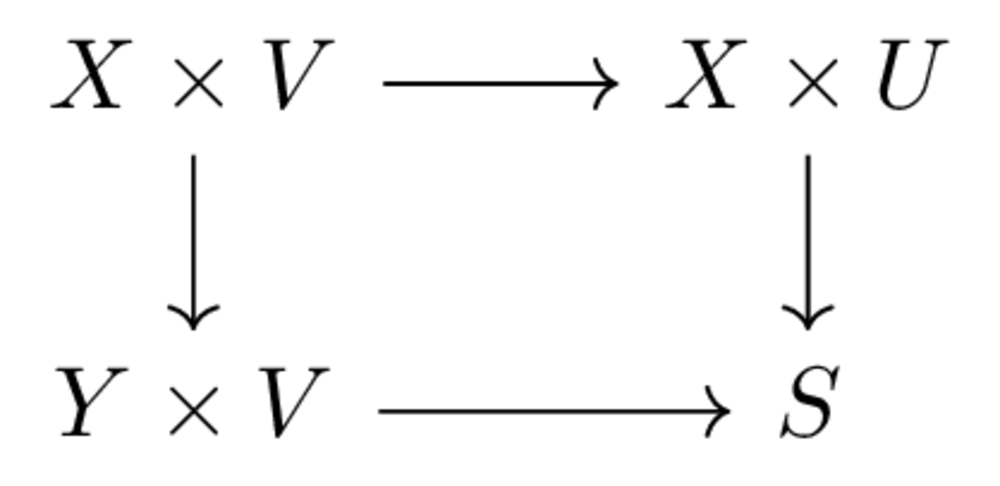
commutes. This defines a category of Chu spaces, called \(Chu(Set,S)\) You can think of a Chu space as a normal-form game. \(X\) is the set of choices available to one player, and \(U\) is the set of choices available to the other. The outcome, given the choices \(x\) and \(u\), is \(e(x,u)\).

You can think of a map of Chu spaces as a way of transforming strategies between the two games. If you would play \(x \in X\) in the original game, you instead play \(f(x) \in Y\). The map in the opposite direction ensures that, no matter what your opponent chooses in the target game, the same outcome could have happened in the domain game - hence your strategy is no worse, in some vague sense (but note that there is no ordering on \(S\), so this does not literally make sense).

The cool thing is that Chu spaces are also a model of linear logic, in a way that sort of reflects “Game semantics for linear logic”, but with some important differences (which we will see).

The duality

The dual of a chu space is simply given by swapping the two sets, i.e \((X,U,e)^\bot := (U,X,(u,x) \mapsto e(x,u))\). This defines a self-duality on the category of Chu spaces, \(Chu(Set,S) \cong Chu(Set,S)^{op}\)

The additive connectives

The additive connectives \(&\) and \(\oplus\) are simply given by the product and coproduct in the category of Chu spaces. Let’s describe this explicitly:

• Given Chu spaces \(A= (X,U,e), B=(Y,V,e')\), their product \(A & B\) is given by \((X \times Y, U + V, e & e')\), where \(e& e'(x,y,u \in U) = e(x,u)\), and \(e&e'(x,y,v\in V) = e'(y,v)\).

  This corresponds to a game where the other player chooses one of the games to play, and a choice in that game. You have to choose a strategy for both games, not knowing which will be played.

• The terminal object is \((*,\emptyset,0)\), where \(0\) denotes the empty function. Interpreting this as a game is slightly weird - it is a game that cannot be played, as the opponent has no moves to make. (Hence if given a choice between this and another game, the opponent must move in the other game, so that this is a unit for the product, as it should be).

• Given \(A\) and \(B\) as above, their coproduct \(A \oplus B\) is given by \((X + Y, U \times B, e \oplus e')\), which is exactly dual to the product. In other words, here the player chooses a game and a move in it, while the opponent must choose a move in both games.

• The initial object is \((\emptyset,*,0)\) - the player cannot move in this game.

The additive connectives, in other words, are much as you would expect from the “game” interpretation. The multiplicative connectives are more weird.

The multiplicative connectives.

The tensor \(A \otimes B\) of two Chu spaces as above is defined by \((X \times Y, [X,V] \times_{[X\times Y,S]} [Y,U], e\otimes e')\), where \(e \otimes e'((x,y),(f,g)) = e'(y,f(x)) = e(x,g(y))\). (Here the last equality is exactly the condition that \((f,g)\) lies in the pullback). In other words, to play \(A \otimes B\), the player simply chooses a strategy in each game. The opponent must choose a strategy in \(A\) which depends on the player’s strategy in \(B\) - a map \(Y \to U\), and vice versa. These conditional strategies must satisfy the condition that, whether we play \(A\) using the strategy matching the player’s strategy from \(B\), or vice versa, we get the same result.

If you squint a bit, this is somewhat like the tensor product of games from before - the opponent can adjust their strategy based on the player’s moves in the other game. But it’s also very different. For example if the two images \(e(X \times U)\) and \(e'(Y \times V)\) are disjoint subsets of \(S\), the opponent has no moves in this game.

The tensorial unit is \(I = (*,S,1_S)\) - in this game, the opponent simply chooses the outcome. Indeed, we have \(A \otimes I \cong A\) - the player’s choice amounts to choosing \(a \in X\), while the opponent must choose a map \(* \to U\) - a point in \(U\), and a map \(X \to S\), which has to equal the map \(x \mapsto e(x,u)\) corresponding to their chosen \(U\), so this is no choice at all.

There is a canonical map \(A \otimes A^\bot \to I^\bot = (S,*,1_S)\). In \(A \otimes A^\bot\), the player must choose a strategy and a counter-strategy. The opponent must choose a map \(X \to X\) and \(Y \to Y\) - of course the canonical choice is the identity. The outcome of this game is exactly the result of playing the player’s two chosen strategies against each other - this is the element \(s \in S\) that the player’s strategy is taken to.

In general, we can identify maps \(A \to I^\bot\) with choices of strategy for the opponent - the point is sent to that strategy, while the map \(X \to S\) is constrained to being exactly the outcome corresponding to that strategy.

Dually, we can identify maps \(I \to A\) with strategies for the player. This of course means that a linear logic proof of the sequent \(\vdash A\) identifies a strategy for the player in the game defined by \(A\).