Cofree dynamical systems and chaos

This blog post largely retraces ideas from Lawvere: Functorial remarks on the general concept of chaos. I saw this in this tweet from Jade Master, which this blog post is basically an extended version of. Hat tip to her.

Let’s try to apply category theory to the study of “dynamical systems”. What is a dynamical system? There are a lot of different versions:

• A discrete dynamical system is a set $S$ with a map $S \to S$.
• A discrete Markov process if a countable set $S$ equipped with a stochastic $S\times S$ matrix.
• A smooth dynamical systsem is a smooth manifold $M$ equipped with a section of the tangent bundle $M \to TM$.

Today, we’ll take the following general view:

Let $\mathcal{C}$ be a symmetric monoidal category, and let $(T,+,0)$ be a commutative monoid in $\mathcal{C}$¹. Then a $T$-dynamical system is simply an object $S$ of $\mathcal{C}$ equipped with an action of $T$, $T \otimes S \to S$.

We think of the elements of $T$ as “time-shifts”, and the composition adds these together. Using this, we can recover a wide variety of different types of dynamical systems:

• Let $\mathcal{C}$ be the category of sets, equipped with the cartesian monoidal structure. Let $T = \mathbb{N}_0$. Then a $\mathbb{N}_0$-dynamical system is exactly a discrete dynamical system in the previous sense.

• Let instead $\mathcal{C} = \aleph_0\operatorname{-}\mathsf{Stoch}$ be the category of countable sets and Markov kernels, and let $T$ be $\mathbb{N}_0$ again (with the usual monoidal structure regarded as a deterministic Markov kernel). Then a $\mathbb{N}_0$-dynamical system is exactly a discrete Markov process²

• Let $\mathcal{C}$ be the category of smooth manifolds with the Cartesian monoidal structure, and let $T = \mathbb{R}$. Then an $\mathbb{R}$-dynamical system is almost the same thing as a smooth dynamical system in the above sense. A $\mathbb{R}$-dynamical system picks out a smooth trajectory $f(-,m) : \mathbb{R} \to M$ for each $m \in M$, in a compatible way. This gives a smooth vector field (i.e a smooth dynamical system in the above sense) $m \mapsto f'(0,m)$.

  This is not quite a 1-1 correspondence, for example because even smooth dynamical systems in that sense can experience “finite-time-blowup”. For example, if we let $M = \mathbb{R}$, then this a dynamical system is just an ordinary (time-independent) differential equation. If we put $f'(t) = f(t)^2$, the unique solution given $f(0) = y_0$ is $\frac{1}{y_0^{-1}-x}$, which goes to $\infty$ as $x \to y_0^{-1}$. So there is no way to find a trajectory, extended for arbitrarily long time, which solves this equation. But on the other hand, perhaps equations like this are bad and shouldn’t be counted. Anyways, they are not dynamical systems in this sense.

Let $Dyn(T)$ denote the category of $T$-dynamical systems - their maps are simply $T$-equivariant maps. There is an obvious forgetful functor $Dyn(T) \to \mathcal{C}$.

Suppose $\mathcal{C}$ is a closed monoidal category. Then the above functor has a right adjoint, which sends $M$ to $[T,M]$. $T$ acts on $[T,M]$ simply by “translation”, i.e $(t.f)(t') = f(t+t')$ To be more formal, the map $T\otimes [T,M] \to [T,M]$ is adjoint to the map $T \otimes [T,M] \otimes T \to M$ given by multiplying the 2 $T$s, then evaluating the hom.

Proof: We claim that $Hom_{Dyn(T)}([M,[T,M']) \cong Hom_\mathcal{C}(M,M')$.

Suppose we have a $T$-equivariant map $\phi: M \to [T,M']$. $T$-equivariance, of course, means that the diagram

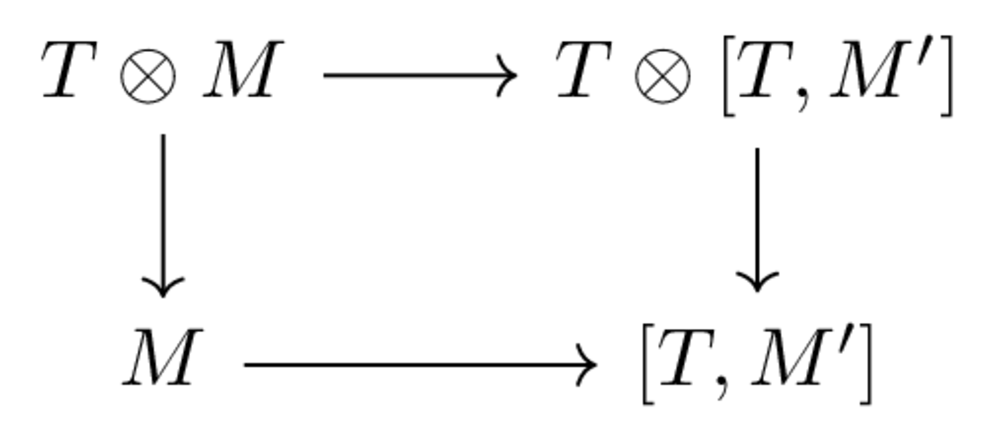
commutes.

The bare map $M \to [T,M']$ corresponds to a map $M \otimes T \to M'$. The above commutative square means that this square commutes:

The bottom way around is “let $T$ act on $M$, then use the map”. The other one is “multiply the $T$s together, then use the map”.

Now let’s insert the unit into the right-hand $T$:

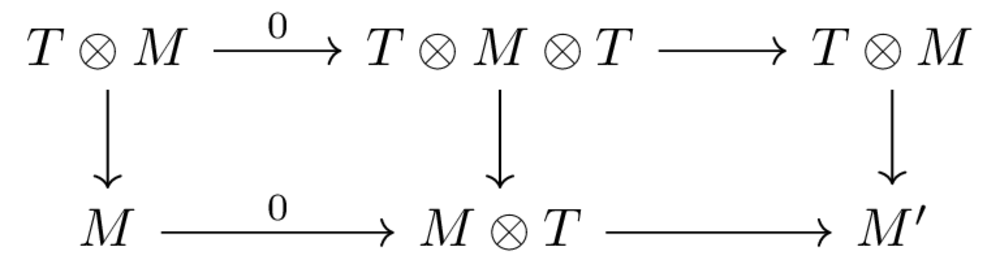
Both these squares commute. And the top arrow is just the identity. In other words the classifying map $T \otimes M \to M'$ must equal the other composite, which is “act, and evaluate at $0$”. Equationally, if $f: M \to [T,M']$, this means $f(m)(t) = f(t.m)(0)$. This means the map $f:M \to [T,M']$ is uniquely determined by the map $M \to M'$ given by evaluation at $0$. On the other hand, it’s not hard to see that any map $M \to M'$ can be extended to an equivariant map by this method. This concludes the proof.

Now, what can we do with these “cofree dynamical systems”³? Here is a cool thing: We can give a categorical definition of chaos.

Let $M$ be a $T$-dynamical system. Let $o:M \to X$ be a map in $\mathcal{C}$ on the underlying space of $M$. We can think of $o$ as an “observable”: some property of the state which we can measure. There is a corresponding map of systems $M \to [T,X]$ which takes each point in $M$ to its trajectory of observations We say $M$ is chaotic with respect to $o$ if map $M \to [T,X]$ is an epimorphism.

If we think of an epimorphism as a “surjection”, this means every possible sequence of observations is possible. In other words, our current observations don’t exclude any possible pattern of future observations.