Notes from "Persistent Homotopy Theory"

My notes from Persistent Homotopy Theory by JF Jardine. The goal of the paper is to study “filtered spaces”. By this is meant in general something like an assignment \(s \mapsto X_s\) of a “space” or simplicial set to each nonnegative real \(s \in [0,\infty)\). A prototypical example is the Vietoris-Rips complex of a metric space, \(V_s(X)\).

The idea being pointed towards is some sort of modification of model category theory to make ideas from persistent homology work more nicely. The main example considered is an inclusion of VR-complexes \(V_s(X) \to V_s(Y)\) coming from an incusion of datasets \(X \subset Y\) where all the points in \(Y\) are “close to” ponts in \(Y\). In this situatio \(V_s(X) \to V_s(Y)\) is not generally a homotopy equivalence or anything like tat, but it’s still a bit “equivalency” - we would like to understand howthis works, and how this plays into classical model category theory.

1 Posets

Given a finite subset \(X\) of a metric space \(Z\), which we think of as a data set, we consider the collection \(P_s(X)\) of subsets \(\sigma \subset X\) where \(d(x,y) \leq s\) for all \(x,y \in \sigma\). We can order this by inclusion - it is exactly the poset of simplices in the Vietoris-Rips Complex \(V_s(X)\).

Now we want to work with this combinatorial data as if it were topological data. This is generally easiest if we’re working with a simplicial set. We can make this into a simplicial set by choosing an ordering on \(X\), but this is non-canonical. We can also consider the nerve \(B(P_s(X))\), but this is somewhat clunky - the resulting simplicial structure is really the subdivision of the complex \(V_s(X)\). (\(B\) for the nerve of a category - a simplicial set - it somewhat unusual notation, but I’ve stuck with Jardine’s choice of notation.)

2 Stability

Define the Hausdorff Distance on finite subsets \(X,Y \subset Z\) of a metric space as follows: \(d_H(X,Y) < r\) if and only if for all \(x\) there exists \(y\) with \(d(x,y) < r\), and vice versa.

Then a situation of interest is if we have two data sets with “small” Hausdorff distance - in this case, the datasets seem to reflect mostly the same underlying topology, so we’d like our methods to give mostly the same results.

What sort of relation do we have between \(P_s(X)\) and \(P_s(Y)\)? For simplicity let’s work with the case where \(X \subset Y\). Then we have an inclusion \(i: P_s(X) \to P_s(Y)\), and we can ask in what sense this is “equivalence-like”. We can try to cook up an inverse by picking a nearest point \(\theta(y) \in X\) for each \(y \in Y\). By assumption \(d(y,\theta(y)) < r\). This means we can build a diagram

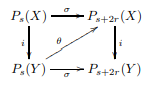
The top square commutes - in other words, \(i\) almost has a retract, except we have to add an extra error of up to \(2r\). The bottom square doesn’t commute - after all, \(\theta\) does really move around some points. But it doesn’t move around points too much - the set \(\sigma(t) \cup i(\theta(t))\) is still in \(P_{s+2r}(Y)\), i.e: the altered points and the original points are all within \(2r\) of each other. The pair of inclusions \(\sigma(t) \hookrightarrow \sigma(t) \cup i(\theta(t)) \hookleftarrow i(\theta(t))\) present a homotopy between \(i\theta\) and \(\sigma\), so the bottom square commutes up to homotopy. In other words, \(i\) and \(\theta\) form a sort of “approximate deformation retract”.

3 Controlled equivalences

In this section we encounter some interesting homotopy theory-ish things. We consider the category of functors \([0,\infty) \to sSet\) (or other categories). We can equip this with the projective model structure, meaning a map is a weak equivalence or a fibration iff it is so sectionwise. This means the fibrant objects are exactly the functors that land in Kan complexes, and the cofibrant objects are precisely those that land in monomorphisms (this is a theorem).

Now the interesting thing we can do is consider various notions of “\(r\)-isomorphism”. The basic motivation for this is that, if \(X \subset Y\) and \(d_H(X,Y) < r/2\), we get a diagram like this

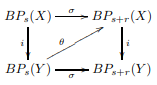
where the top triangle commutes, and the bottom commutes up to a homotopy fixing \(NP_s(X)\) - an “\(r\)-interleaving”

This tells us that the maps \(\pi_n(BP_s(X)) \to \pi_n(BP_{s}(Y))\) is “almost an isomorphism”:

• We can find a preimage for any element in \(\pi_n(BP_s(Y))\), as long as we’re willing to increase the allowed error by \(r\).
• If two elements in \(\pi_n(BP_s(X))\) agree in \(\pi_n(BP_s(Y))\), they also agree in \(\pi_n(BP_{s+r}(X))\)

Let’s call something like this an \(r\)-isomorphism.

We can then ask in general for an \(r\)-equivalence, which gives an \(r\)-isomorphism on the (filtered) homotopy groups. These maps have various good properties

• They are stable under composition with weak equivalences
• They’re not quite stable under composition, rather when composing an \(r\)-equivalence and an \(s\)-equivalence, you get an \(r+s\)-equivalence.
• They satisfy a similarly modified version of the 2 out of 3 condition.
• A pullback of an \(r\)-equivalence which is a fibration is a \(2r\)-equivalence (and a fibration).
• If a map is an \(r\)-equivalence and a sectionwise cofibration (not the same as a cofibration in the projective model structure!), it admits a \(2r\)-interleaving, in the sense of the diagram above.

This gives a sort of bizzarro model structure/homotopy theory for \(r\)-equivalences. In this world, an \(r\)-interleaving is a bit like a deformation retract.