Left adjoints preserve colimits.

Let’s prove a classical theorem (Emily Riehl’s favorite!) from category theory: Right adjoint functors preserve limits. So let’s assume we have categories \(C,D\), functors \(F: C \to D, G: D \to C\), and a natural bijection \(C(G(a),b) \cong D(a,F(b))\). Let’s also fix a diagram \(X: I \to C\) from some index category \(I\). Now recall that a limit of \(X\) is an object \(\lim X\), equipped with maps \(\pi_i: \lim X \to X(i)\), so that every triangle

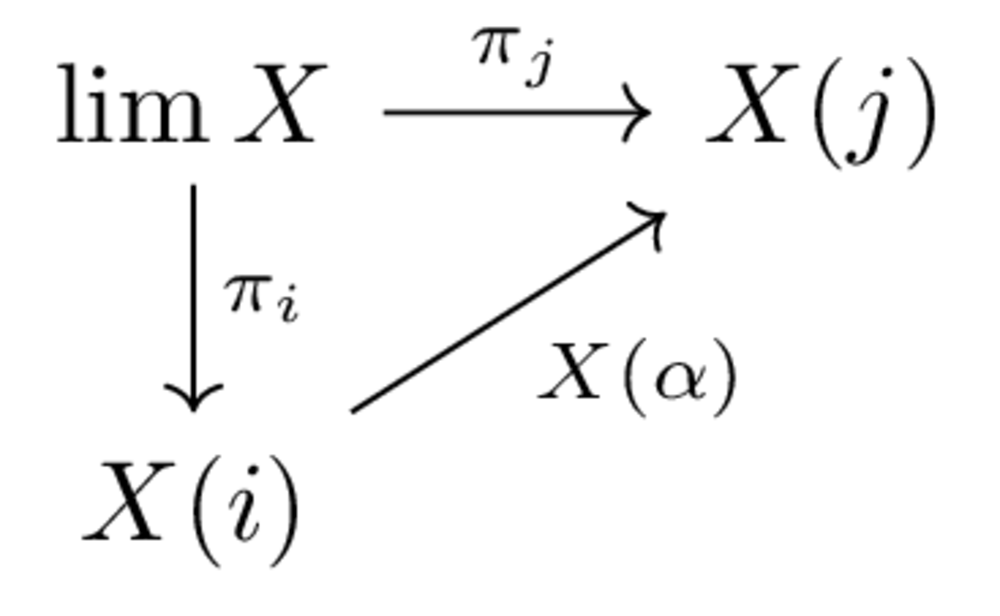
commutes, and so that, given another set of data \((p, f_i: p to X(i))\) with the same property, there is a unique map \(f: p \to \lim X\) so that \(f_i = \pi_if\).

(I am sort of assuming you already know about limits, and just writing the definition above for convenience).

The proof idea, very weakly formulated, is that the adjunction lets us control maps into \(F(b)\), and the universal property of the limit is precisely about maps into \(F(\lim X)\).

Let’s first make completely precise the claim: it is that, supposing \((\lim X, \pi_i)\) forms a limit of \(X\), then also \((F(\lim X), F(\pi_i))\) forms a limit of \(F \circ X\). Note that this makes sense - \(F(\pi_i)\) really is a map from \(F(\lim X)\) to \(FX(i)\).

Now let’s fix another cone \((p,f_i)\) on \((F\lim X, F(\pi_i))\). We are attempting to construct a map \(p \to F(\lim X)\). This is equivalent to a map \(G(p) \to \lim X\). We’re going to construct that map by constructing maps \(G(p) \to X_i\). Where do we get those maps? We apply the adjunction again - they are simply the mates of the maps \(p \to F(X_i)\) we started with. Now we need to confirm that the map \(p \to F(\lim X)\) actually does make the desired triangles commute.

This follows from naturality of the adjunction, using the same property for \(G(p) \to \lim X\): Consider the composite \(p \to F(\lim X) \to F(X(i))\). By naturality of the adjunction (with regard to postcomposition), the mate of this map is the composite \(G(p) \to \lim X \to X(i)\). By construction, this equals the input map \(G(p) \to X(i)\), which is the mate of the original \(f_i: p \to F(X_i)\). Hence the composite has the same mate as \(f_i\), so equals it.

The second thing we need to prove is that this map is unique with this property. We can do this by noting that, given two distinct map with this property, their mates \(G(p) \to \lim X\) are distinct (because the correspondence is bijective), and both have this property (by the same argument used above). This establishes the claim.