The homotopy theory of groups

Context: Krause and Nikolaus: Group Theory for Homotopy Theorists (pdf). Krause and Nikolaus develop group theory using model categories (well, one model category). This is obviously a joke, but I think it is a very useful pedagogical joke. So I’m going to go through it and try to explain what’s happening.

Group presentations

If you’ve taken a course on group theory, you’ve probably learned about presentations of a group. Here are some examples:

• \(\langle s,r | r^4, s^2 srsr \rangle\)
• \(\langle a, b | \rangle\)
• \(\langle a, b | aba^{-1}b^{-1} \rangle\).

On the left of the pipe, we have a set \(S\) of generators. On the right of the pipe, we have a different set \(R\) of relations - these are “group words” in the generators, i.e words involving both the generators and their inverses. The meaning of such a “presentation” is that it describes a group, namely the quotient of the free group on \(S\) by the relations.

Every group \(G\) has a presentation (in fact, many), for example given by taking \(S = G\) and \(R\) given by all words which evaluate to \(1\) in \(G\). This leads to the idea that one could define group theory out of presentations. This seems to work out well - in fact, given \(G,H\) groups, if we take their “canonical” presentations as above, a group homomorphism \(G \to H\) is exactly the same thing as a function \(G \to H\) which takes those words in \(G\) which evaluate to \(1\) to words in \(H\) which evaluate to \(1\).

However, this doesn’t work in general - most group presentations don’t have “enough generators” to represent all group homomorphisms into the presented group. And there are many maps which “should” be group isomorphisms which don’t have an inverse on the level of presentations.

Model categories

The basic things you can do in a model category are:

• Invert certain maps that “should” be isomorphisms (or “equivalences”)
• Replace an object with a “better behaved” one which is “equivalent” in that sense.

Let’s take a more classical example from “real” homotopy theory: Simplicial sets. In this context, we think of a simplicial set \(X\) as a “model” for a topological space, its geometric realization \(|X|\). A map \(X \to Y\) is a simplicial homotopy equivalence if the map of spaces \(|X| \to |Y|\) is a homotopy equivalence of spaces. However, in many cases, such an equivalence can’t be inverted, even up to (simplicial) homotopy. Similarly, there are often maps between geometric realizations which can’t be represented by maps between the simplicial sets, even up to homotopy.

The basic solution to this is to work with certain nice simplicial sets called Kan complexes. A Kan complex has “enough simplexes” so that all the maps between them that “should” exist, do. Now we could simply work with the category of Kan complexes - but this is an inconvenient category. Its main deficiency is probably that it does not have all colimits. This is compared to the full category of simplicial sets, which is as nice as they come.

So we use a powerful piece of technology called a model structure, making simplicial sets into a model category. (This is usually called the Kan model structure, or the Kan-Quillen model structure).

The upshot of this is that every simplicial set is homotopy equivalent to a Kan complex, in a very structured way which lets you use the technically convenient structure of the whole category of simplicial sets to describe “the homotopy theory of Kan complexes”.

Back to groups

Now we are going to try to adapt the above to groups.

The way to do this is to describe the trivial cofibrations - essentially, these will be those maps which are “morally group isomorphisms”.

Using the machinery of model categories, we can get away with specifying only a small “generating family”. These are on page 2 of the paper.

Now here’s a fun fact: this small list pins down exactly the “proper” presentations of groups, in this sense:

Theorem: The following two are equivalent for a presentation \(\langle S \mid R \rangle\)

• The map \(S \to F(S)/R\) is bijective, and \(R\) contains every word which is zero in \(F(S)/R\).
• For every diagram

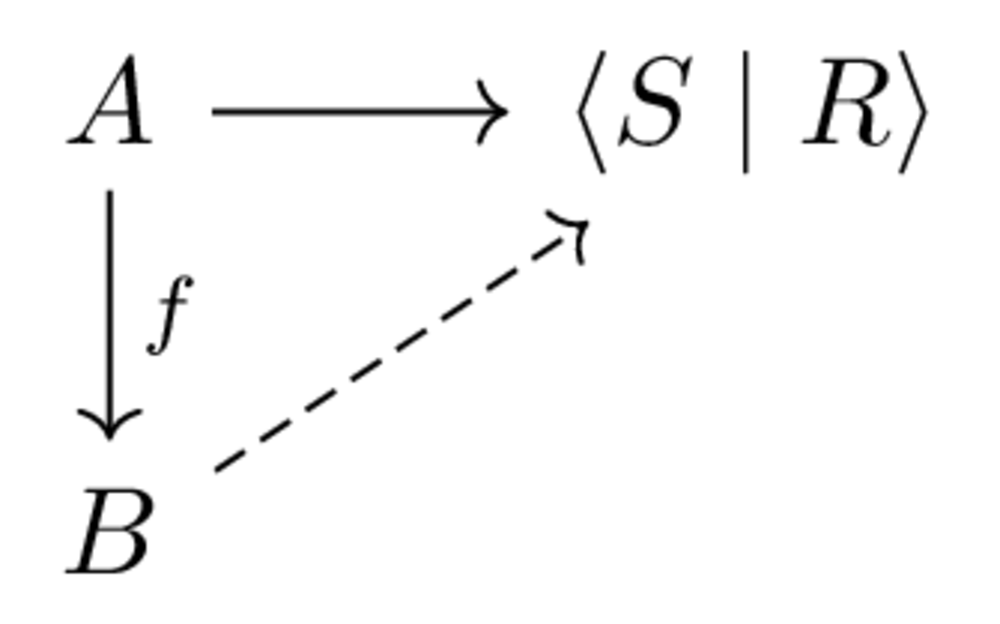
if \(f\) is in the generating list, there exists an extension like the dashed arrow making the triangle commute.

Proof: First, it’s easy to check for each type of generating arrow that this holds:

• \(a\) and \(b\) must be sent to the same element (by injectivity), so we can simply send \(c\) there as well.
• We can extend the map by sending \(a\) to whatever element \(w^{-1}\) evaluates to.
• The remaining three maps simply add relations which are derivable from the existing ones - hence their images must already be in \(R\).

Now for the other direction, suppose \(a,b \in S\) go to the same element in \(F(S)/R\). Then the map \(\langle a,b \mid ab^{-1} \rangle \to \langle S \mid R \rangle\) does not have an extension over the first generating map. Hence that map is injective. Suppose \(w \in F(S)/R\) is not in \(S\). Then the map \(\langle S \mid \emptyset \rangle \to \langle S \mid R \rangle\) does not extend over \(\langle S \sqcup \{a\} \mid a w^{-1} \rangle\) - there is nowhere to send \(a\) (since it must be sent to something that goes to \(w\), for the property to hold). The statement that \(R\) contains every word that goes to zero means that \(R\) is stable under certain operations, which can similarly be proved from the morphisms.

It follows from the general theory of model categories that there always exists a map \(\langle S \mid R \rangle \to P\) into a “nice” (in technical terms, fibrant) presentation, which is itself a trivial cofibration. Understanding what the trivial cofibrations are in technical terms is more complicated - an argument going in the other direction from the one above will show that they are exactly those which correspond to group isomorphisms, but this might be a bit tricky.