The zero-one laws of Kolmogorov and Hewitt–Savage in categorical probability [zero-one-laws-paper]

TLDR

This is a post about my paper The zero-one laws of Kolmogorov and Hewitt-Savage in categorical probability, joint with Tobias Fritz. This is a "companion piece" where I try to explain those ideas in a more understandable language. There are essentially three ideas in this paper:

- "Markov categories for synthetic probability theory" - this is only treated briefly, since this is just the background that we're building on top of. Tobias has a long paper on this, A synthetic approach to Markov kernels, conditional independence and theorems on sufficient statistics. - "Kolmogorov products" - a take on tensor products of infinitely many objects. These are introduced into the framework to handle probabilistic systems with infinitely many variables. - "Zero-One Laws". These are theorems from probability theory of the form "If an event A satisfies ..., then P(A) \in 0,1" - i.e either it always happens or it never happens. For two classical ones, Kolmogorov's and Hewitt-Savage's, we give a way of phrasing them in the categorical language and prove them.

In this post, I'll try to give an accessible take on these ideas. I'll assume some familiarity with category theory, and a _very_ small amount of familiarity with probability theory

What do you mean, "synthetic probability theory"

Synthetic vs analytic

(This is a weird rambly section. Feel free to skip it)

Think about plane geometry for a moment. Let's contrast two approaches: In the "Euclidean" approach, we work without any reference to what a point, a line, and so on, _is_[^fn:1]. We simply have certain axioms which relate lines and points, certain properties (like congruence) which things can have or not have, and so on. We could also call this approach _formal_, or maybe _syntactical_. We can contrast this with how plane geometry might be treated in the modern world:

- A point is an element of \mathbb {R}^2. - A line is a subset of \mathbb {R}^2 such that ...

and so on. Here a point is really a particular _thing_, so is a line, and the statement "The angle ABC equals the angle CBD" is defined in terms of the things that A,B,C,D are, rather than being a more or less irreducible notion. We call such an approach _analytical_. Another way of looking at it is that Euclidean geometry admits several distinct models (particularly if we abandon certain axioms, e.g. the parallel postulate). On the other hand, the analytical approach of \mathbb {R}^2 augmented with some structure is a _specific_ model.

Markov categories

The classical approach to probability theory is analytical - a probability space (\Omega ,\Sigma ,P) is a specific thing with a specific structure. We want to contrast this to a synthetic approach to probability theory. One "model" of our synthetic approach will be "classical probability theory", i.e measures and \sigma algebras. Another model will be given by "possibility theory", where each outcome either happens or doesn't happen. And there are many other exoctic models like that.

This approach is called Markov categories. It is a notion which has been developed by several different authors under different names - see the paper by Fritz above for a review of the literature (and a much more in-depth treatment of Markov categories).

A Markov category is a symmetric monoidal category (\mathsf {C},\otimes ,I), where the monoidal unit is terminal, where each object X \in \mathsf {C} carries a distinguished cocommutative comonoid structure \operatorname {copy}_X: X \to X \otimes X, \operatorname {del}_X: X \to I and such that the symmetric monoidal structure isomorphisms are homomorphisms[^fn:2]. See Tobias' paper for an unpacking of this definition.

The interpretation of a Markov category is that the objects are "spaces" that our random variables can take values in, and the maps are "stochastic processes" or "kernels", i.e functions which produce their output somewhat randomly. The tensor product of two objects X \otimes Y is the "product space" where points are pairs of points (x,y) - but note that this is _not_ a product in the categorical sense, since, give a random map A \to X \otimes Y, we can not in general recover it from the "marginals" or "projections" A \to X and A \to Y. This is because the random values of X and Y may be _dependent_. On the other hand, we do have "diagonal" maps X \to X \otimes X - which non-randomly send x to (x,x) - and a "projection" map X \to I, which is actually unique (there is precisely one way to randomly generate an element of the one-point space).

A map I \to X is called a _distribution on X_, and should be thought of as the abstract version of a probability measure. For instance, if P:I \to X is a distribution, and f: X \to Y is a map, then we can make sense of this diagram:

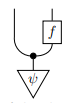
it is the distribution on X \otimes Y where x \in X is sampled according to \psi , then y \in Y is sampled according to f(x). Note the bullet which denotes the copying operator.

We can define a few different standard terms from probability theory in this context.

Independence

Given a map f: A \to X \otimes Y, we can ask whether X,Y are /independent given A /. The intuition here is that given some a \in A, if I sample (x,y) from f(a) and tell you what the x was, that gives you no information about the y (given that you know what the a was). In diagram form, this looks like this:

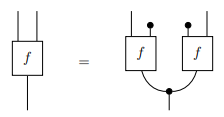
The basic idea here is that it makes no difference whether we generate (x,y) together in one go, or separately (using the same a).

Determinism

A map f: A \to B is _deterministic_ if we have this equality:

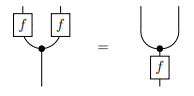
This means if we run f twice with the same a \in A, we get the same b \in B out. This is a reasonable definition of "deterministic".

Note that in both these cases, the existence of the comonoid structure is _exactly_ what we needed to make sense of the probabilistic notion.

Examples

- There is a Markov category \mathsf {Stoch} where the objects are measurable spaces, and the maps are Markov Kernels

- There is a Markov category \mathsf {FinStoch} where the objects are finite sets and the maps are stochastic matrices. It is a full subcategory of \mathsf {Stoch}. - There is a Markov category called \mathsf {SetMulti} where the objects are sets and the maps are "total relations", i.e relations X \to Y where each element x \in X is related to at least one element in Y. - There is a Markov category \mathsf {Gauss} where objects are natural numbers, and maps n \to m are "affine maps \mathbb {R}^n \to \mathbb {R}^m plus constant Gaussian noise"

For (many) more examples, see Tobias' paper.

Infinite tensor products

Most theorems in probability theory involve infinite families of variables. To make sense of that in our framework, we need to make sense of "distributions on infinite product spaces", which means we need a notion of "infinite tensor product". The definition goes like this: Let \{X_j\}_{j \in J} be a collection of objects in a markov category \mathsf {C}. For each finite subset F \subset J, we can make sense of the tensor product \bigotimes _{j \in F} X_j[^fn:3]. Since the tensor unit is terminal, we have natural maps \bigotimes _{J \in F'} X_j \to \bigotimes _{j \in F} X_j for each inclusion of finite sets F \subset F'. Then we can ask for a cofiltered limit of this system:

\lim _{F \subset J} \bigotimes _{j \in F} X_j

This is a reasonable definition of "infinite tensor product", which we can denote \bigotimes _{j \in J} X_j However, it turns out we need one more condition. The issue is that in a Markov category, having an object defined up to isomorphism is not always good enough - we want it up to _deterministic isomorphism_, so that the comonoid structure is determined as well. The natural condition to add to make sure we pick the "right" limit is that each of the projections \bigotimes _{j \in J} X_j \to \bigotimes _{j \in F} X_j, for each finite subset, is deterministic. Such an infinite tensor product, we called a _Kolmogorov product_.

Kolmogorov's Zero-One Theorem, abstractly

With this setup, it turns out it's very easy to prove an abstract version of Kolmogorov's Zero-One Law. Informally, the content of the law is this: suppose you have a family (X_n) of independent random variables, and some event A which is determined by these variables, but is independent of any finite subset of them. Then P(A) \in \{0,1\}

Here is our abstract version: Let (X_j)_{j \in J} be objects so that the Kolmogorov product \bigotimes _{j \in K} exists. Let p: A \to \bigotimes _{j \in J} X_j be a map, and s : \bigotimes _{j \in J} X_j \to T be a deterministic map. Suppose p displays the conditional independence of the X_j given A, and that for every finite F \subset J, the joint distribution

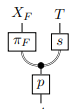
displays the independence of X_F and T given A. (Here X_F = \bigotimes _{j \in F} X_j). Then the composite sp : A \to T is deterministic.

I will sketch the proof (see the paper for details). Essentially, we first prove that T is independent of all the X_j, not just the finite subsets. To see this, we note that the definition of independence is comparing two maps into T \otimes \bigotimes _{j\in J} X_j. This is a limit, so it's enough to show that all the component maps, which are the maps for finite F \subset J, agree - this is true by definition. Now it follows by a string diagram manipulation that sp satisfies the definition of determinism:

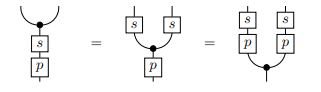
This concludes the proof.

To recover the classical Kolmogorov 0-1 law, we must do a little bit of technical work. We work in the Markov category \mathsf {BorelStoch} of _standard Borel spaces_. This Markov category has countable Kolmogorov products[^fn:4]. We let A = * and let our X_j be the _spaces_ that the variables X_j from the theorem take values in. We let the map p give the joint distribution of the variables. We let T = \{0,1\}, and we let s be the indicator for the event. Then the theorem says that the composite sp is deterministic. So the probability that sp is 1, which is the probability that the event happens, is either zero or one.

[^fn:1]: Euclid actually did try to define notions like lines, points, etc, but we're gonna use his name anyways [^fn:2]: Note that we're not assuming all maps, or even all isomorphisms, are homomorphic. This makes Markov categories an evil notion [^fn:3]: I am handwaving some non-issues with regards to non-strictness here [^fn:4]: It turns out that proving this is significantly harder than proving the abstract theorem, once you have the setup

Backlinks

A response to Maudlin on credence and chance [a-response-to-maudlin-on-credence-and-chance]

Credence - and chance - without numbers (and with the Euclidean property) is a philosophy paper by Tim Maudlin. In it, Maudlin discusses the closely related notions of _credence_, the subjective likelyhood that a specific agent associates to some outcome, and _chance_, the objective likelyhood that the event happens. He argues that

  • The traditional approach of measuring these outcomes with numbers is wrong, but
  • this shouldn't trouble us too much, because we can do a lot without them.

As it happens, I have my own serious reservations about the traditional measure-theoretic formulation of probability (due to Kolmogoro). By I still think this paper is more or less terrible. Maudlin displays a Wikipedia-level understanding of the paradoxes surrounding infinity in probability theory. His proposed solution amounts to enumerating a list of properties that an agent's system of credence should satisfy, and arguing that these axioms suffice for the things we usually want to do with "subjective degree of belief". This is actually fine such as it is, but his description of this is also seriously lacking.

Infinity in probability theory

There's the following very classical paradox in probability theory: Suppose you toss a dart at a dartboard. For each point p on the dartboard, we can ask for the probability that the dart hits that exact point p. Suppose we have no relevant information about the tossing process, so that each point seems equally likely. What is the probability P(p)? Well, it can't be more than zero, because then the total probability, the probability that the dart hits any point, would be, not just greater than 1, but infinite! This is because there are infinitely many points on the dartboard, and any positive number added to itself infinitely many times is infinite. But hold on, it also can't be 0, because that means by a similar argument that the probability that the dart hits any point on the dartboard is also 0 - but it must hit _some_ point.

First I'll note that this problem actually is _not_ entirely resolved by measure theory. Measure theory allows for a uniform probability measure on continuous spaces like the interval [0,1] (by, essentially, not allowing us to add probabilities up in every case. More on this later). But if we just suppose a countable dartboard, we're left with the same problem.

But, hang on, does a dartboard really have an infinite number of points? And what does it mean for the dart to hit a point? Certainly the point of the dart _itself_ has a non-infinitesimal area, so that if we partition the dartboard into "points" of that size, there will be a finite number, each of which we can assign some positive probability without issue. In general, any area on the dartboard, no matter how small, has a positive probability of being struck by the dart, and this remains true no matter how small we make the dart, as well.

In other words, this paradox hinges on an infinitesimal dart, as well as an infinitesimally accurate measuring tape with which to measure the coordinates, which presumably has infinitely long numerals on it (presumably the person assigning these credences has an infinitely large brain as well, to be able to hold in their minds the coordinates pointing out a specific point on the dartboard to infinite precision).

Any mathematician knows that you have to handle a situation like this _very carefully_. You cannot expect to apply your intuition directly and get consistent results. I am actually kind of surprised to find serious philosophers making this kind of argument in 2020. This is on par with saying that Zeno's paradox proves you can't use numbers to measure space (or time).

To be fair to Maudlin here, I do think he has a point: there do seem to be situations where you should be indifferent between a (countably) infinite number of outcomes, and probability theory won't let you do that. Dartboards is just a bad example.

Maudlin's shaky relationship with infinity shows up again in his discussion of the classical Kolmogorov approach to probability. He cites the definition of a _finitely additive_ probability measure, and not the \sigma -additive (or countably additive) version used by every probability theorist and statistician in the world. Then he criticizes it for only being finitely additive!

He also critizises the use of a \sigma -algebra, arguing that it seems irrational to exclude certain sets from consideration. I think Maudlin needs to spend a small amount of time understanding non-measurable sets before arguing they're stupid. For one thing, a nonmeasurable subset of \mathbb {R}^2 (such as we might ask "will the dart hit a point in this subset or not" of), is _extremely weird_. It's consistent with ZF minus Choice that there exist no such sets. Certainly such sets always contain regions of "infinite complexity", in the sense that there are (non-infinitesimal) regions of the dartboard so that, if the dart hits there, no finite amount of measurement will suffice to determine whether it is in the set or out of it. Indeed, it's not too far off the mark to think of the \sigma -algebra as denoting the "determinable" events.

The fact that a probability measure is only _countably_ additive is still a bit weird. You can make philosophical arguments for this choice: To check whether a \in \cup _n A_n, we can check whether a \in A_n for each a - and this is guaranteed to give you an answer in a finite amount of time, but only if you're taking a finite union. There are reasonable counterarguments to this, but Maudlin doesn't engage with this topic at all - it really seems as if he doesn't realize that mathematicians have been taking infinite disjunctions of events all this time[^fn:1].

Maudlin's solution

Maudlin's proposed replacement for numbers is essentially the following idea: it's not required that a person's credences be represented by some definite "thing" - a number or another mathematical object. Instead we should ask about the _structure_ on the system of credences, and what rules this should follow for any "rational" person.

This is actually a very good idea! Structuralism! Defining things extrinsically rather than intrinsically! I like this approach.

Let's go over the basic principles that Maudlin comes up with. The paper is short on rigor, but since it's a philosophy paper and not a math paper, I won't hold that against it.

- The set of "credences" should have a partial order[^fn:2]. - The map \operatorname {Cr} which assigns an event its credence should be order-preserving - in other words, if event P entails the event Q, then \operatorname {Cr}(P) \leq \operatorname {Cr}(Q). - There should be a least credence \bot and a greatest credence \top , corresponding respectively to the credence in an event which is certain not to happen or certain to happen (say, a contradiction and a tautology). - The map \mathrm {Cr} should have the following property: if P \Rightarrow Q, \operatorname {Cr}(P) = \operatorname {Cr}(Q),

then \operatorname {Cr}(Q \wedge \neg P) = \bot . This is the so-called "Euclidean property" that Maudlin cannot stop going on about: "the whole is greater than the part", or in this case, if P entails Q, and it's possible that Q but not P (i.e. Q does not entail P), then our credence in Q must be _strictly greater_ than our credence in P.

We can define a partial addition operation on credences, denoted \oplus in the paper, by setting \operatorname {Cr}(P) \oplus \operatorname {Cr}(Q) = \operatorname {Cr}(P \vee Q) whenever \Cr (P \wedge Q) = \bot . It's not exactly clear in the paper whether we extend this using the equality on credences - for example, whether we can assign a value to \operatorname {Cr}(P) \oplus \operatorname {Cr}(P) by finding some other event Q so that \operatorname {Cr}(P) = \operatorname {Cr}(Q), \operatorname {Cr}(P \wedge Q) = \bot , and setting \operatorname {Cr}(P) \oplus \operatorname {Cr}(P) = \operatorname {Cr}(P \vee Q). This seems a harmless enough extension (if we really regard credences as _equal_, and not just equivalent in some sense, it seems inevitable), but Maudlin doesn't really spell it out. Nevertheless the addition is still _partial_, since, for example, when rolling a fair dice, we can't add our credence in the event "The result will be one of 1,2,3,4" to itself, since there is no mutually exclusive event which is equally likely. This is not really a bug - indeed, while you can add probabilities and get a number greater than 1, you can't really treat that number _as a probability_.

So far, Maudlin's approach differs from the Kolmogorovian approach chiefly in that he lets the poset of credences be any ordered set, not just numbers, and that he doesn't require the order on credences to be _total_ - we can have no opinion about the relative plausibility of two events without declaring them _equally_ plausible. This is reasonable enough. Probably the weirdest thing here is that the "Euclidean property" is _also satisfied by Kolmogorov probability!_ The reason that adding a point to a set doesn't change the probability that the dart will land there is simply that it's impossible that the dart will land at that precise point. This is obviously counterintuitive (and there are ways of defending it, and counterarguments to those, and so on - but Maudlin does not engage with this at all), but that is the classical approach. It does not seem to violate the Euclidean property at all.

Having the addition in hand, we can actually reformulate the Euclidean property simply as "\oplus is cancellative", i.e if C \oplus D= C \oplus D' then D = D'. This means that \operatorname {Cr}(Q) = \operatorname {Cr}(P) \oplus \operatorname {Cr}(Q \wedge \neg P), and if this equals \operatorname {Cr}(Q) then \operatorname {Cr}(Q \wedge \neg P) = \bot , since \bot is the unit of addition.

Now Maudlin wants to talk about _relations_ between credences. First of all I have to go on a rant about his whole discussion about ratios. Mathematics has come a long way since Euclid, and citing him like you actually believe his axioms provide a sound formal basis of geometry is not gonna convince anyone that you know what you're talking about. Maudlin goes oddly pedantic and says that the ratio of a circle's circumference to its diameter is not \pi , but rather, the ratio of the number \pi to the number 1, and this is in general what people mean when they identify a ratio with a number. I'm glad to hear that Maudlin has found a solution to the long-standing problem of the identity of mathematical objects (presumably resolving it in favor of a _very_ strong form of Platonism?), but I couldn't find this in the bibliography of the paper or any of his other work. Until I do, I have to insist that "loose talk" is when you insist that two mathematical objects identified under isomorphism cannot possibly be called equal, not the other way around.

Okay, rant done. We can define the ratios between credences by addition. For example, we can say that credence C is twice as big as credence D if C = D \oplus D. Maudlin, quoting Euclid: "Magnitudes are said to have a ratio to one another which can, when multiplied, exceed one another". There is however a serious problem with this: the partiality of addition means that you can't _compare_ these ratios, and many pairs of credences have no ratio to one another, even though Maudlin insists that they do.

Let's pull back here a bit. Suppose I have an ordered (commutative) monoid (M,\leq ,+). Then I can say that m,m' have a ratio to each other if there exist n,n' \in \mathbb {N} so that n.m \geq m', and n'.n' \geq m. If this is true, we can actually obtain a unique real-numbered ratio "m/m'" as the supremum of all n/n' \in \mathbb {Q} so that n.m' \leq n'.m.[^fn:3] Here I'm using n.m to denote the n-fold sum m + m + \cdots + m.

Now, this _doesn't_ work for credences - even in situations where it feels like it should[^fn:4]. The increasingly accurate rational approximations to the "true" real ratio requires longer and longer chains of addition, but this is generally impossible to define for credences. We can define what it means for C/C' to be an integer - namely that n.C' = C. We can also _sometimes_ define what it means for C/C' to be a rational number - for example if 2.C = 3.C', we can say C/C' = 2/3. But if e.g. C = \top , there's no way to make this work. And, crucially, we can't usually compare ratios with each other either - otherwise, we might have argued that expecting number representations for each ratio is too much.

As it stands, by Maudlin's (or rather, Euclid's) definition of ratio, there is no ratio between \top and any event with "probability greater than 1/2" (speaking informally - of course credences aren't probabilities and so on), in contrast with how Maudlin uses it.

This is an area where the paper could really have benefited from some rigor. It's not clear whether Maudlin means to tack on "ratios" as a primitive notion - so that, in addition to having a "more likely than" relation on credences, we have ratios between certain pairs of credences, which can be compared.

All these issues could be solved _very easily_, by imposing some extra structure on the model. For instance we could add "formal sums" of credences which don't have a sum, and say that the statement 2.P \geq Q makes sense even when 2.P is not defined as a credence.

Closing

As I mentioned above, I actually, genuinely think it's a good idea to think about replacements for classical probability theory. In some sense my own work on Markov categories is a version of this, a sort of "synthetic probability theory". Much like Maudlin, Markov categories start by asking "what structure do we actually need to do the job of probabilities?". They go in a very different direction, not least because we actually care about the job that probabilities do for people in the real world, but the spirit is actually similar.

But stress-testing your theory by applying it to situations involving infinity - without working rigorously with infinity _at all_ - is bound to get you into trouble. Frankly, if the only problem your theory solves is that it makes sense of infinite conjunctions, it's basically useless. Infinite conjunctions only come up in abstrac mathematical models, and trust me, those guys aren't really looking for a new theory. In the real world, it's very hard to write down infinitely many statements and think about your credence in the statement "one of these is true".

The mathematical idea in this paper - which, again, I actually don't think is a stupid idea - could have fit in a couple of pagers, including a fair amount of exposition and the easy fixes to the problem mentioned above. The philosophical work here seems mainly to be a takedown of traditional probability, which falls woefully flat.

[^fn:1]: A less elegant reason for asking for countable composition but not general infinitary composition is that it leads to a useful, theoretically convenient theory, but still allows for measures like the uniform measure on the interval. This is just an argument from practicality - we take these axioms instead of some others because they make the calculations work out - so I won't hold it against Maudlin if he doesn't take this argument very seriously [^fn:2]: Maudlin seems to not know this term, which probably could have cut several pages from his exposition [^fn:3]: Ironically, in the usual construction of real numbers, they are limits of ratios (between integers), so one could make a convincing argument that a real number really is literally a ratio. [^fn:4]: Credences can be "infintesimal, in the sense that we might have n.C \leq C' for ALL n. That's not what I'm talking about."